It takes two to entangle – A tea-time diversion through Quantum Physics
Published 23 March 2022
Foreword
As with all new technology, it gains acceptance through awareness and familiarity. We are entering an era where the ubiquitous term Quantum Technology is being touted as the solution for all our needs. In many ways quantum technology can and will provide some amazing new capabilities which will affect many areas of our lives, but like all technologies it has its limitations.
Quantum physics is not something the average person ever realises they come across in their everyday lives and so it is still shrouded in a veil of mystery and seemingly magical effects, not to mention a rather large amount of advanced mathematics!
This book aims to enlighten the reader to this exciting new realm without the typical barriers of complex jargon and bewildering formulae.
If you put the book down having learnt something new and exciting, then I consider my job done. Enjoy!
Dr Matt Himsworth
Principal Quantum Scientist, Quantum Sensing, Cyber Information and Systems Group, Dstl
About the Defence Science and Technology Laboratory (Dstl)
Dstl is an executive agency of the Ministry of Defence (MOD) providing world class expertise and delivering cutting-edge science and technology for the benefit of the nation and allies. Dstl supplies specialist services to MOD and wider government, working collaboratively with external partners in industry and academia worldwide, providing expert research, specialist advice and invaluable operational support.
Dstl has been supporting quantum technology, both fundamental and applied, since 2013 with funding from Centre for Defence Enterprise. This was followed by the Quantum Landscape Document, which highlighted the many opportunities this field could provide to Defence and Security, as well as funding a number of demonstrator projects in quantum-enhanced position, navigation and timing.
The £350m UK National Quantum Technology Programme (UKQTP) was set up in 2015, resulting in four Quantum Technology Hubs. Dstl has been involved in most aspects of the UKQTP from its outset and renewal in 2019, as well as advising major industrial projects.
The need for future quantum engineers has always been a high priority, and Dstl has funded a cohort of 41 PhD studentships in 2014 and another 25 in 2019.
Internal expertise has also grown with the opening of the state-of-the-art Dstl quantum laboratory in 2020.
Dstl has provided support to the recently commissioned National Quantum Computing Centre, and the National Metrology Institute led by the National Physical Laboratory (NPL).
Introduction
This guide is what we call a Biscuit Book, something you can pick up and dip into with a tea and biscuit. The Biscuit Book is arranged as a series of easily digestible chunks that each cover a topic and doing so in a manner that provides the essential information without ever being too technical.

Mug and plate of jaffa cakes on a desk
The most appropriate snack to accompany this book would be the Jaffa Cake. It reflects some of the stranger aspects of quantum physics in which objects can be both solid particles and tenuous waves at the same time – just like a Jaffa cake can be considered simultaneously both a cake or a biscuit[footnote 1].
The first thing we want to remind you when encountering quantum physics is:
DON’T PANIC
To quote the Hitchhiker’s Guide to the Galaxy by Douglas Adams.
This is because quantum physics is often seen as a complex and frequently unintuitive subject that is primarily based on a lot of advanced mathematics. To overcome this hurdle, we will attempt to unravel these mysterious phenomena by providing familiar examples and analogies.
We aim to give you a ‘feel’ for quantum mechanics and the opportunities that the resulting technology can bring without jotting down a single equation or remembering an endless list of acronyms. For each aspect of quantum behaviour we provide an example or two in how this relates to current and future technologies.
We hope you find the Biscuit Book both informative and digestible, although we do not suggest dunking it in your tea!
What makes something ‘Quantum?’
At the beginning of the 20th century, physics provided a huge advancement to our understanding of the nature of the universe with the developments of special and general relativity, quantum mechanics, and the resulting discovery of elementary particles, fields, and forces. These were such momentous breakthroughs that all physics discovered prior to this time was termed ‘classical’ in the same way as classical antiquity separated two eras of civilisation.

Image of blackboard with equations written on it including E=mc squared
Much of what we intuitively understand and experience every day is often grouped under the term classical physics. These are effects like a piece of toast falling due to gravity, how light reflects off a window, or how your cup of tea cools down when left to stew for too long. Essentially, most of the physics you may have learnt in school. These theories[footnote 2] haven’t changed for over a century because they can be explained mathematically and will reliably predict the behaviour of objects around us. Physicists still use these ideas when describing effects at ‘everyday’ scales.
But (there’s always a but), as our technology keeps advancing and we become able to probe down to smaller and smaller scales, we find these classical, comfortably- intuitive, principles sometimes start to fail. In the early nineteenth century, results that came out of experiments on atomic-scale processes baffled the greatest minds of the time (and the not so great minds as well).
The insight that finally explained all of these results was identified essentially by playing around with different forms of mathematical equations until they matched the experimental results. Physicists then reverse-engineered the equations to figure out what the underlying theory should be. It was akin to knowing that 42 was the answer to the “ultimate question of life, the universe, and everything[footnote 3]”, but being less certain on the question itself. And lo, quantum mechanics arrived on the scene!
Quantum mechanics is the mathematics that describes and predicts the behaviour (actions and interactions) of atoms and the sub-atomic particles inside them. These objects can have dimensions smaller than a billionth of a metre, although quantum behaviours have been seen in objects a thousand times larger. Throughout this book we will refer to these ‘quantum[footnote 4] objects’ simply as particles.
There are four main points you need to know about this theory that we will keep referring to throughout this book:
- It is a theory of waves, but not oscillations of physical things like water and sound. It describes waves of probability. A peak in the probability wave means something is probably there, and a trough means it probably isn’t there.
- “Lies, damned lies, and statistics!” There are random fluctuations in some properties of particles when measured. What we can reliably predict with quantum mechanics is the statistical average of many identical measurements on a single particle (or the average of single measurements on many identical particles).
- The ‘quantum’ in quantum mechanics relates to the discrete values that some properties (such as energy, momentum or electric charge) of a particle appear to be divided up into. This affects how atoms absorb and emit electromagnetic radiation, transport sound and heat, and form chemical bonds.
- Finally, we don’t have a clue what makes particles behave as they do (if there is a reason). However, the resulting mathematics matches with observations from experiments better than any other theory of physics has ever matched experimental results. It has been shown to agree with the data to parts in a trillion!
Quantum behaviour
Let’s start with a quote from Arthur C Clarke:
Any sufficiently advanced technology is indistinguishable from magic.
This could have been written specifically about quantum technology and how it advertised to have miraculous properties and the potential to solve every problem in modern life. Alas, it is not magic, but just very strange compared to our everyday experiences of nature. Its public relations are not helped by the dense and advanced mathematics that surrounds and deters the casual onlooker from gaining a deeper insight.
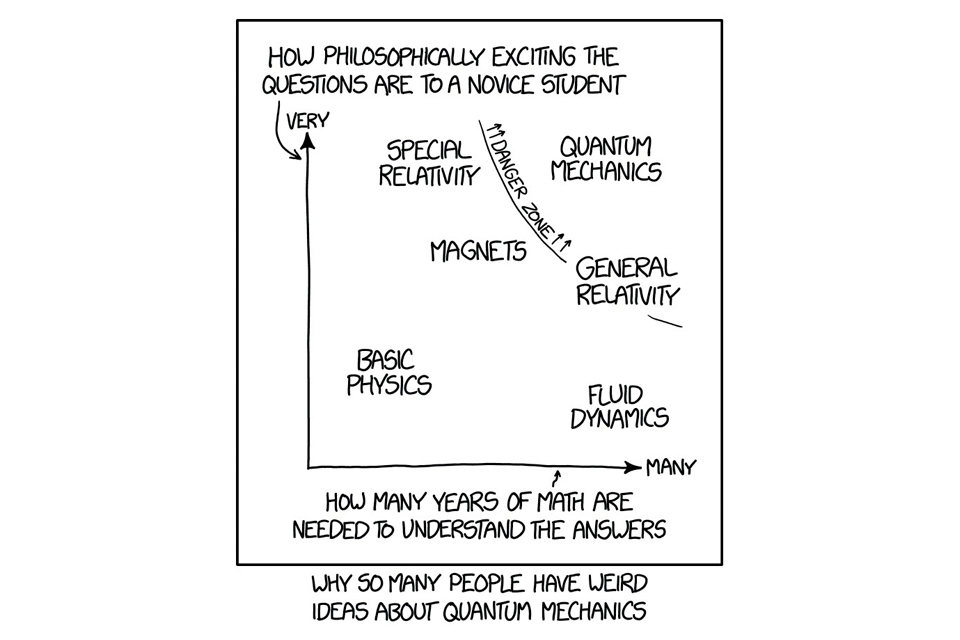
Chart showing why so many people have weird ideas about quantum mechanics, plotting how philosophically exciting the questions are to a novice student against how many years of math are needed to understand the answers.
In this book we are avoiding complex technical jargon and mathematics so we will present the physics in terms of how particles appear to ‘behave’ during any of the fundamental processes via analogies and examples. This will hopefully provide some level of intuition into what quantum physics can and cannot do.
A quick definition of terms:
- Quantum Physics encompasses all the effects and behaviours we see at the smallest scales.
- Quantum Mechanics is the mathematical theory we use to describe the physics.
- Quantum Technology is the application of quantum effects for practical use.
Formally, quantum mechanics is a part of the more general quantum field theory which also combines classical field theory and special relativity, but not general relativity (that has proved too hard to include so far and would lead to a ‘general theory of everything’).
Quantum technology is nothing new. It is part of our everyday lives and has been for decades. Examples include:
- Lasers (and how the internet is connected)
- Nuclear power
- Semiconductors (and all modern electronics)
- Global Positioning Systems (via atomic clocks)
- Magnetic Resonance Imaging
- Quantum dot display technology
The progress of quantum technology is commonly split into 3 phases:
Phase 1
- Understanding of how quantum mechanics affects the structure of materials
- Understanding how atoms, molecules and materials interact with fields and forces
- 20th century quantum technology
Phase 2
- Controlling quantum mechanical effects in order to engineer devices that enhance the performance of current methods
- Processes such as superposition and wave/ particle duality
- Underpins most of the technology developed during the second half of the 20th Century
- Currently the focus of investment and commercialization
Phase 3
- Developing new methods that rely solely on quantum effects
- Processes such as squeezed-state measurements and entanglement.
- Currently the focus of investment in R&D with the purpose of moving beyond the limits of classical technologies
Each phase of quantum technology builds upon the last, starting with understanding how quantum physics affects the materials and processes we experience, to manipulating those process to get new and exciting forms of technology.
We have split up these behaviours into sections that loosely relate to the three phases of quantum technological progress:
- ‘Place your bets’ looks at the statistical and quantised properties of particles and fields and how they affect interactions in matter.
- ‘Neither here, nor there’ explores how the wave/ particle nature of quantum systems leads to new ways of controlling particles and their interaction with their environment.
- ‘Giving it 110%’ describes the effects that are truly strange and are only possible with quantum physics, and how they can be used to move beyond ‘classical’ limitations.
01 Place your bets
Quantum mechanics is a theory based on statistics. The result of any single measurement cannot be known for sure, only the probability of an event occurring can be calculated. Nevertheless, this seemingly unpredictable character of nature at its most fundamental level ultimately results in highly predictable classical processes.
The reason why we can rely on it is because of the sheer numbers of particles involved[footnote 5] which average out seemingly irregular behaviour. In this section we explore the building blocks of quantum mechanics such as the wavefunction and the uncertainty principle.
Particles
Throughout this book, as with many of the other books on this subject, we talk about quantum effects happening to ‘particles’. This is just a shorthand for any object that can be affected by processes that can only be described by quantum physics.
At the very smallest scales (smaller than a hundredth the width of a human hair) this means all matter. Specifically, we are either discussing atoms (particles that make up the solid/ liquid/gaseous matter around and within us) or photons (particles that transfer energy and forces in the form of electromagnetic radiation, i.e. light). Both exhibit quantum effects and interact with each other in a manner that is best described by quantum mechanics.
For quantum technologies, the particles that are most commonly encountered are:
Photons

Integrated components for photonic information processing. Image credit: University of Southampton.
Atoms

A cloud of laser cooled strontium atoms (small glowing ball at the centre) within a lattice clock. Image credit: University of Birmingham.
Ions

Two-module quantum computer prototype at the University of Sussex. Image credit: Sussex Ion Quantum Technology Group.
Superconductors

Superconductor-based quantum computer. Image credit: IBM.
Crystals

A diamond crystal doped with nitrogen vacancy centres. Image credit: Element6.
Probability
Quantum mechanics involves calculating the probability of events occurring. The ‘state’ of a particle cannot be defined with complete certainty until it is measured, only its probability of being in the state can be predicted. An everyday example is playing the lottery. As soon as you have bought a ticket you are in a state of being both a winner and (more likely) a loser. You exist in this combined state until a measurement is made – the lottery draw.
In quantum mechanics, we can calculate the average result of many measurements very accurately, but we cannot predict individual results for certain (i.e. we cannot know who will win the lottery, but we can know the odds[footnote 6]). An alternative, and perhaps more useful, approach is to perform a single measurement on many identical particles. This is the same as many identical measurements on a single particle[footnote 7].
Nuclear power relies on the probabilistic decay, or fusion, of the elements. We cannot predict the time every particle will decay, but we can use the statistics to harness these events for reliable and efficient energy production. The image shows the inside of a nuclear fusion reactor which may provide clean and sustainable energy production.

Image credit: iStock.com/ MARHARYTA MARKO
The wavefunction
Quantum mechanics is a theory of probability waves and therefore every particle, whether it be an electron, photon, or a towel, is treated as if it were a wave. Why this is how nature appears to behave at small scales is anyone’s guess, but the mathematics fits the observations found in experiments as perfectly as we can measure them.
The wavefunction is a mathematical object that defines the physical properties of a particle (such as position, energy, momentum, etc.). By plugging the wavefunction into other formulae we can determine the properties at different times and positions as well as their response to external fields and forces. The wavefunction can be interpreted as an oscillating wave whose amplitude defines the probability of the object in having the above properties. Because the particles act like a wave, they can exhibit effects such as interference, superposition and tunnelling which are the cause of many seemingly strange quantum effects.
Another quirk of the wave-function model is that the boundaries of the particle (the edges) are less distinct. The amplitude of a particle’s wavefunction would tend towards zero as its classical dimensions finish, but the wavefunction never actually reaches zero. This means that there is always some vanishingly small, but non-zero, chance of the wavefunction existing everywhere. This property of nature at the smallest scales is responsible for why quantum physics leads to seemingly impossible effects, like passing through brick walls. These are, of course, probabilistic effects that usually only occur at the smallest scales, so no need to worry about falling through your armchair.

Artistic illustration of waves and sub-atomic particles inside an atom
The uncertainty principle
One of the most fundamental and key properties of quantum mechanics is the (Heisenberg’s) Uncertainty Principle that states that some pairs of observable properties of a particle cannot be measured with equally high precision at the same time. Pairs include Energy/ time, Momentum/ position, and Phase/amplitude. Irritatingly, the more precisely you measure one property, the less accurately you can measure the other.
The reason for this lies in the wave nature of quantum theory, but the mathematics is like any other type of wave, such as water, light, and sound. Therefore we can provide an example of the uncertainty principle found in the classical understanding of sound waves:

Image credit: iStock.com/ shironsov
Imagine a single musical note being played on a keyboard. The pitch of the note is related to the energy bound in the vibrations it produces in the air (higher pitch means faster, more energetic, vibrations). Let the note play for a long time. An accomplished musician can identify the note with a high accuracy. However, what if we ask “when is the note?” The longer it is played, the harder this is to pin down. Conversely, if the note is played for a very short time, the musician’s ear drum has barely had time to vibrate and so the pitch of the note is less certain. Therefore we have the uncertainty principle between energy (pitch) and time.
This effect is seen in any wave-like, or periodic, process and as quantum mechanics treats all objects as a wave, the effects of the uncertainty principle are much more apparent and important.
Spin
Spin is very important in determining how atoms and other particles interact with each other and with electromagnetic fields (such as light and magnetism). During the development of quantum mechanics it was noticed that some particles appeared to have another, unexpected, degree of freedom[footnote 8] which acted as if it was spinning. This ‘spin’ took discrete values (it is quantised).
For example, a steel bolt can have several degrees of freedom (such as direction, position, motion etc.), and also has two discrete spin directions about its long axis; rotating clockwise or anticlockwise.
However, in quantum mechanics the objects are so small they can’t actually be spinning because the rate would be sufficiently high to break the law of relativity. We don’t actually know what the spin is physically – it is just some inherent property like electric charge or mass – but for all intents and purposes one can think of it as a spinning top which spins clockwise or anticlockwise.
The spin of an atom affects how it behaves under the influence of a magnetic field. New magnetometers based on warm atomic vapours now compete in sensitivity to superconducting magnetometers (also based on quantum effects). These new sensors are small enough to make wearable magneto- encephalograhy (MEG) systems.
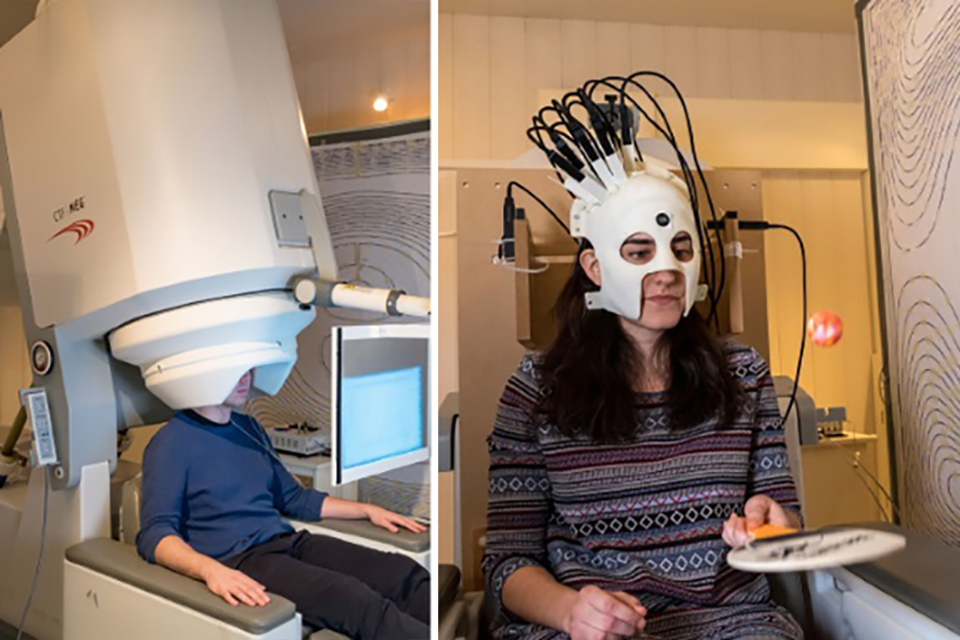
The image on the left is a cryogenically cooled magnetometer in which the patient has to sit very still. The image on the right shows a special headset with multiple room temperature atomic magnetometers that can provide the same sensitivity but also whilst the patient is moving. Images courtesy of the University of Nottingham.
Atomic energy levels
The energy an electron contains within an atom is dependent on the diameter and shape[footnote 9] of the space it ‘occupies’ around the nucleus[footnote 10]. The electron cannot take on just any value of energy; only discrete quantised values are possible – known as electron orbitals. Without the restriction of quantisation keeping the electron within an orbital, its negative electric charge would be uncontrollably attracted to the positive nucleus. The outcome of this would be no atoms existing in the universe at all, so we are lucky quantum mechanics exists!
An analogy would be the limited harmonics (musical notes) one can produce on a stringed instrument. This is because the strings are bound at either end of the instrument, just as electrons are bound to an atomic nucleus by electromagnetic attraction. This quantisation via bound waves exists throughout all matter and determines many of the properties of materials, such as structure, heat flow, appearance (i.e. shiny, transparent), and electrical conductivity, to name a few.
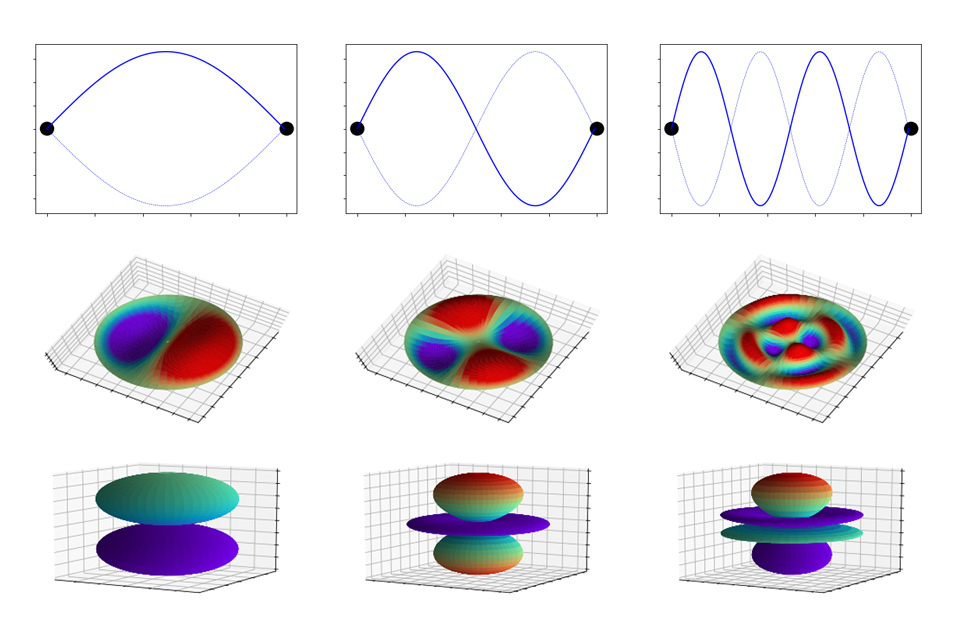
The vibrational ‘modes’ of bound waves. Top row: 1D waves such as a guitar string bound at the black circles. Middle row: 2D waves such as a drum bound on the edges. Bottom row: 3D waves like electrons orbitals bound to the nucleus. Image credit: Dstl (Crown Copyright)
Interactions with light
We experience the world primarily through light and how it interacts with materials around us[footnote 11]. We only see a small fraction of the full electromagnetic spectrum which stretches from low energy radio-waves and micro-waves, through infra-red, visible and ultraviolet light, all the way to high energy x-rays and gamma rays.
All interactions of matter at the atomic scale involve exchanges of electromagnetic waves. First, one should note that the colour of the light (as determined by its oscillation rate, or frequency) determines the energy in the light wave. If a wave oscillates faster, it will be more energetic[footnote 12], so blue light has a higher energy content than red light.
Light can be absorbed by an atom, causing it to transition from a lower to higher energy level (or electron orbital), and vice versa when the atom emits light. This resonant transition only occurs over a very small range of energies, so the atom can only be excited with exactly the right energy (frequency), no more, no less. It is these resonant transitions which are used in nearly all quantum technologies, as their frequencies can be affected by their environment[footnote 13], whether it be gravitational or magnetic fields, or by interaction with other atoms.
Many quantum technologies rely on probing atoms, ion, or crystals with lasers. Atomic clocks provide the most accurate and stable time sources. These are vital for communications, navigation, power distribution and financial trading, to name a few. The image shows a chip- scale atomic clock in which all components have been shrunk to smaller than a grain of rice.

Image credit: John Kitching / NIST
Not forgetting about that poor cat …
We can’t end this section on the building blocks of quantum physics without mentioning Edwin Schrödinger and his unfortunate cat.
The (thought) experiment is to place a cat inside a box together with a vial of poison that is released when a radioactive element decays. The decay time is random so we cannot tell if the cat is dead or alive without looking inside the box (this is the measurement). If the cat-box-poison system [footnote 14] obeys quantum mechanics then there is a probability that the cat is in a combination of both dead and alive[footnote 15].
This, fortunately untested, experiment was meant to highlight all of the strangeness of quantum mechanics when we start applying it to normal every-day objects which have definite properties and are not fuzzy and ‘wave-like’ from our experience[footnote 16]. It also introduces us to the concepts of superposition and entanglement which we shall meet in the next two sections.
Let us finish this section with a quote from Sir Terry Pratchett:
In fact, the mere act of opening the box will determine the state of the cat, although in this case there were three determinate states the cat could be in: these being Alive, Dead, and Bloody Furious.
02 Neither here, nor there
One of the main differences between classical and quantum physics is that the particles we think of as solid objects in classical physics can act like waves in quantum physics, and vice versa. This distinction (or confusion) is one of the major properties that gives quantum technology many of its unique capabilities. In this section we will explore how this wave/ particle duality can be used to enhance processes, and we will also discuss the limitations of quantum measurements due to decoherence.

Drawing that can look like a rabbit or a duck, shown within a line chart with rabbit on one axis label and duck on the other.
Wave/ particle duality
So which is it, are quantum objects waves or particles? The poetic answer is “not either/or, it’s both and more”. From our experience, particles (or any solid object) have hard edges and distinct properties such as position and mass. Particles generally can’t be split apart without destroying their nature. Waves on the other hand are more indistinct and we rarely attach labels on the mass or exact position to them. Also waves can be split, interfered and recombined without significant consequences.
One must remember that quantum mechanics is a (probability) wave theory, so everything must be treated mathematically to some extent as a wave, but it is also clear that some objects have hard edges that hurt when you drop them on your toe. Whether we treat something as a wave or a particle essentially depends on what process you are exploring.
A good example is light. At school we learnt light is a wave and exhibits wave-like properties such as refraction, diffraction and interference. However, when scientists look at light interacting with an atom it behaves as a pulse (quanta) of energy – the photon – which we treat as a particle. This is because the atom can only absorb a discrete ‘quanta’ of energy to be able to transition from one energy level to another.
As a good rule of thumb, one should think of an object in quantum mechanics travelling as a wave, but interacting as a particle.
One property of light that is normally only associated with solid objects is momentum – a property usually requiring mass which photons do not have. However, photons can impart momentum and so produce a force on other objects. In the image we see a comet with two tails. One is from the path of the comet, but the other fainter tail is due to the pressure of sunlight on the trail of ice crystals.

Image credit: iStock.com/ shaunl
Superposition
If we have an oscillating wave, such as light, it is possible to split the light along different paths and recombine it. When peaks of two waves meet they form larger peaks, and when a peak meets a trough the resulting wave flattens out. This is known as interference. Very small differences between waves become very apparent when they interfere and therefore interferometers make, arguably, the most sensitive measuring devices available17.
As quantum mechanics treats any particle as a wave one can, in principle, create interference between nearly any properties of a single particle (superposition) or between many particles (entanglement). These properties could be position, velocity, energy, electron state, momentum, to name a few. When a measurement of the particle’s property is made, it will settle into a single value.
How does this provide a useful function in quantum technology? Well, interferometers that use waves of light are only sensitive to changes in length, whereas waves formed of atoms (known as matter-waves) are also sensitive to electric and magnetic fields, gravity, rotations, and accelerations. This makes them advantageous for sensing and metrology applications.
The wave nature of atoms means they can be placed in a superposition and have interferometry performed on them, just like optical counterparts. Because atoms have mass measure forces such like gravity, which has negligible effect on photons. These ‘atom interferometry’ systems are now becoming commercial devices

Field-compatible Absolute Quantum Gravimeter developed by Muquans. This picture was taken on Mount Etna volcano as part of the H2020 project Newton-g. Image credit: www.newton-g.eu
Tunnelling
A particle’s wavefunction does not have clear physical boundaries as does, say, a snooker ball. It is difficult to determine exactly where it begins or ends. This means that as you move away from the particle the probability of it sharing space with you becomes increasingly unlikely, but never zero.
Fundamentally this is a general property of any wave (classical or quantum) and you can experience the effect with light for yourself:
Fill a glass with water and hold it lightly in your fingertips below the water line. If you look down in the water at the correct angle you will not see your fingers tips on the inside of the glass, only a mirror-like reflection called ‘total internal reflection’. This is due to the change of refractive index18 between the glass and the thin layer of air between the glass and your fingers. Light cannot penetrate this interface. Now squeeze the glass in your finger- tips as tight as your dare (don’t break the glass!). You should just be able to see your finger-tips penetrating the reflective surface as you squeeze that layer of air out. The light is now tunnelling to your fingers and back.
This example is called a frustrated, or evanescent wave, but the process is the same in quantum tunnelling. When a particle meets a thin impenetrable barrier, there is a non-zero probability that the wavefunction can extend beyond the barrier and interact with objects on the other side. Devices can be engineered to enhance and control this effect, such as tunnel-effect transistors, and tunnelling is a key process in nuclear fusion in stars. It is this effect which ultimately limits the size and density of components on a current microchip technology because as they get smaller and closer together, the chances of tunnel increases leading to errors in chip processes.
Tea transfer through tunnelling

Illustration of two cups, with hot liquid passing through their walls from one cup into the other
With classical physics the only way to transfer the tea to the empty cup would be by tilting the cup or by heating it and hoping some would bubble across (shown in purple, also known as thermal annealing). With quantum physics there is a finite chance the tea ‘wavefunction’ (red) can pass through the walls of the tea cup. Fortunately this is very unlikely otherwise the tea would go everywhere.
D-Wave is a type of quantum annealing computer that uses tunnelling. This means that the computer can perform calculations that involve finding the lowest energy state of a system. This is useful for applications that have several possible answers but one wishes to find the optimum answer. Uses such as finding the fastest delivery routes, the most efficient fabrication process, air traffic control, artificial intelligence, or perhaps designing better quantum computers.
A good analogy is trying to find the lowest point in a large farmer’s field. We could wait for it to rain and look for where puddles form. However, the field might be quite uneven and several puddles form, so which is the lowest? To avoid waiting a long time for all the water to slowly diffuse to the lowest puddle, quantum tunnelling could provide a faster route to find the answer.

A superconducting quantum annealing chip. Image credit: D-wave
Decoherence
This subject is related to the question “If quantum mechanics is the underlying physics of all matter, why don’t we notice these strange effects?” This is the age old conundrum of where the boundary lies between quantum and classical physics[footnote 19]. Quantum effects are most apparent when superpositions exist. The bloody furious cat we met earlier demonstrated that a particle can be in several states simultaneously and only by measuring the particle will it settle, or collapse into a single state. The act of measuring involves finding some information about the particle’s properties (its state).
A ‘measurement’ sounds like an intentional act, but it could also be caused by some unwanted interaction with the surrounding environment that forces the superposition to collapse; such as a change in temperature of the apparatus or electrical noise within a control system. For a particle in a superposition, if there are more chances for it to interact with its environment then the probability for it to collapse into a single state will also increase[footnote 20]. In every second of every day we are measured by our interactions with the rest of the universe, such as touching an object, feeling the warmth of the sun, or listening to music.
Coherence is a description of how predictable the state of a wave is at a later time or position. The loss of superposition causes abrupt changes in the wave-like nature of the particle and leads to decoherence. This is an unwanted effect in quantum technology and is the main hurdle to overcome in quantum computing where decoherence must be severely minimised.
Back-action
This goes somewhat deeper into the effect the measurement itself has on the quantum state of the system. Does the detector affect the quantum state if the process of the measurement itself involves quantum effects? When I shine light onto an atom to find its position, the light will place a small force on the atom, thus slightly changing its position. This is the back action of the measurement.
This means that it is nearly impossible to remove the effect of the observer [footnote 21] out of the processes you are measuring and this puts a limitation on the amount of information we can usefully obtain. Whilst it may seem an unwanted side effect, we can sometimes use this perturbation to adjust the evolution of the wavefunction in an engineered manner as we will find out in non-demolition measurement later.
For example, assume we are batch cooking biscuits. As any baker will tell you, timing is critical but we have a new oven and so don’t know exactly how long we should bake for. To judge how well the bake is going, we carefully open the oven door slightly and prod the nearest biscuit. In doing so we can decide whether to adjust the cooking time or temperature. We haven’t ‘measured’ any of the other biscuits but have sacrificed a few biscuits to optimise the final result (a non-demolition measurement). However we can’t be absolutely perfect in our culinary skills because the act of opening the oven several times will have disturbed the uniformity of the temperature inside the oven (this would be the back action). The more we check, the less uniform the batch of biscuits will be. The precision of our baking will always be limited by the uncertainty principle.
03 Giving it 110%
Quantization and wave/ particle duality provide a wealth of new tools to engineer future technologies, but quantum physics has a couple more tricks up its sleeve. By a clever application of the uncertainty principle, it is possible to improve the sensitivity of measurements by overcomingclassical limitations on the level imposed by the fundamental noise in the system, thus providing the ‘extra 10%’ beyond current performance potential. The final tool is the ‘spooky’ connectivity between particles that can be engineered via entanglement that have absolutely no classical counterpart.
Squeezed states
What would it be like if you could sweep all of your mess under the carpet? The house would look good for just long enough while you impress an important visitor. Wouldn’t this be a useful trick in a measurement where you hide all that annoying noise somewhere where it won’t bother you? This can be a reality in quantum mechanics.
First, remind yourself of the uncertainty principle. A squeezed state is when we use this effect to construct a system where all of the noise (uncertainty) is directed into the unwanted (and unmeasured) partner.
Producing a squeezed state practically is very difficult to do and has only been demonstrated in a handful of experiments. The important aspect is that the system has to be designed so that as little information as possible can be gained from the unwanted partner, either on purpose or by accident. Using our analogy it is very hard to hear a short burst of sound from a keyboard without getting some clue of the pitch.
Squeezed states are most beneficial in devices that use interferometry, where fluctuations in the amplitude and phase of the waves affect the fundamental sensitivity of the system. A current focus of the Laser Interferometric Gravitational Wave Observatory (LIGO) is to increase sensitivity by incorporating optical squeezed state measurements.

LIGO Lab. Image credit: Caltech / MIT https:// www.ligo.caltech.edu/ image/ 201701814a
Quantum limit
This subject follows on from the squeezed state idea. If we can increase the accuracy of a measurement by shoving all the noise elsewhere, how much improvement is possible? Nature sets two limits, the ‘shot noise limit’ which bounds the accuracy of any classical measurement, and the ‘quantum (or Heisenberg) limit’ which bounds a quantum measurement.
Both limits are actually a result of the uncertainty principle. To understand the difference between the two limits let us look at the measurement of light intensity measured by a photodetector. Light is an oscillating wave and so the amplitude (height) of the wave depends on where along the wave you measure it. The position along the wave is known as the phase (is it at a peak, trough, or somewhere in between?). Our classical detector cannot measure the amplitude and the phase independently; the two are always mixed together.
Statistical fluctuations (from quantum physics) result in uncertainties in the amplitude and phase, and when mixed together we detect the shot noise of the measurement. If we are able to build a system in which only information on the amplitude of the wave can be extracted whilst rejecting all information on the phase – a squeezed state – we are left with the statistical fluctuations solely in the amplitude of the wave. This residual noise is known as the quantum limit. Note that it is not noiseless, you are still at the mercy of the statistical nature of reality at the quantum scale[footnote 22] and the back-action of the measurement.
Non-demolition measurement
Earlier we learnt that it takes many repeated measurements to find a statistically consistent result. We can do this in two ways:
- Perform many identical experiments on a single particle, or
- Perform the same experiment on many identical particles.
The problem with the first method is that once you have measured the particle you have extracted all the information you can get. There are no further useful measurements you can make without having to reset the entire system for the next experimental run. The second method, however, provides you the opportunity to measure only a few of the particles at a time, whilst maintaining the superposition of the others. One cannot extract an exact answer due to the random fluctuations of the few particles, but you can get an estimate of what the answer might be.
An analogy might be coin-tossing. If I get 100 people to simultaneously flip a coin, I can collect all the results and find that the chances of getting a ‘head’ is 50% with an uncertainty[footnote 23] of ±5%. Imagine instead, if I got all 100 people to flip a coin but asked only ten of them what their result was. From that small sample I might find that the average is 60% ‘heads’ but with an increased uncertainty of ±10%. It’s not the same as measuring all 100 people’s result, but it might be close enough for a useful estimate. In the second case I have made a measurement without ‘demolishing’ the full quantum state (we have only demolished 10% – a mere scuff).
This is not a way to cheat decoherence, as the purity of your quantum state is reduced whenever you extract information from it. This means that the precision of the final results will be slightly lower than if we hadn’t taken a sneak peak of the result.

Hand with coin balanced on finger and thumb, ready to flip
This technique can be used when you need to actively adjust the system during the measurement with minimal back-action on the quantum state. For example if our quantum sensor is moving out of range of the dynamic limits and must be shifted back within range (if a magnetic field got too strong, or a gyroscope rotated too quickly). In this case you would only need a small amount of information of the quantum state extracted to keep it approximately within range.
For some measurements, the longer you measure the lower the noise, or uncertainty, in the result. However, in quantum physics the measurement process is destructive, so quantum non-demolition measurements (QNDM) provide a way to extend your measurement period with minimal disturbance of the system. This is especially true in time-keeping, where scientists have used QNDM to extend their measurement period by over a factor of 7.

A strontium ion atomic clock. Image credit: National Physical Laboratory
Entanglement
I advise popping the kettle back on and getting some more biscuits before we address this subject. This is probably the strangest of quantum effects and there exist no analogies in the classical world to give you an intuitive insight of how it works. Technically, entanglement is a strong correlation between particles produced by an interaction at some point in their past. It was discovered as theoretically possible when physicists explored the consequences of the mathematics of quantum mechanics in the 1930’s but took until the 1980s until it was finally observed.

Image credit: iStock.com/ dimitris_k
The process results in properties of two or more particles being highly correlated, no matter the distance they are separated. Correlation is nothing special from a classical standpoint, but it is that last phrase that makes entanglement uniquely strange. After the particles are entangled, if I make a measurement on one it will have an immediate (as far as we can tell) effect on the other, no matter how long or far they have been separated. Moreover, the information is (apparently) transferred between particles faster than the speed of light can travel. However, the properties of the particles obey the usual quantum random fluctuations, so you cannot tell something has changed in the second particle without comparing (or correlating) it to the first[footnote 24]. This requires normal, classical, lines of information flow. This prevents entanglement being used for faster-than-light communication.
So how does the state of one particle transfer to the other during entanglement? This is still a mystery. There are some theories that suggest time passes differently for the entangled pair compared to the rest of the universe, or even that time itself results from entanglement. These ideas have yet to be tested.
Quantum physics provides new ways of imaging via the use of single photons or effects such as entanglement. This may provide methods of looking round corners or through obscurants, imaging at hard to reach wavelengths, high resolution long distance covert ranging, or even ghost imaging where the light never interacts with the object under inspection (see the following image and figure).

A ‘quantum hologram’ in which an image is transferred from one entangled laser beam to another. Image credit: University of Glasgow
Entanglement in action
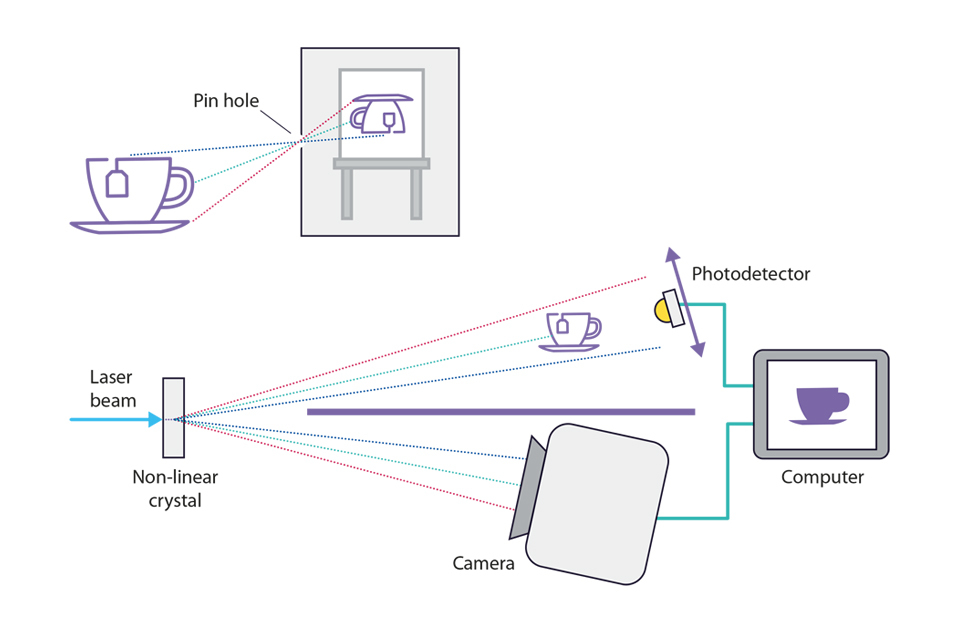
Depiction of a pin hole camera capturing an image of a cup of tea, followed by a depiction of a laser beam being used to capture an image of a cup of tea.
Top image: A pin-hole camera analogy helps explain the effect of ghost imaging. Light reflecting off the tea cup and then incident on the picture frame can only take one path due to the small hole in the wall, as indicated by the different coloured light rays, resulting in a sharp image of the teacup.
Bottom image: Ghost imaging. The laser beam coming from the left is split into pairs of photons by a crystal (pairs have the same coloured paths). The paths of each pair are entangled so there is a one-to-one relationship between the direction of the photon reaching the camera and the direction of the photon illuminating the teacup. The single pixel photodetector can move up and down and records a ‘click’ when a photon reaches it without being blocked by the object. By correlating the ‘clicks’ with the camera image, a computer can reconstruct an image of the object even though the light incident on the camera has never interacted with the object being imaged. The entanglement at the crystal acts like the pin-hole in the top image.
Teleportation
We are most familiar with this phrase from science-fiction in which an object, or person, can be completely transferred from one place to another. Unfortunately this is not possible with quantum physics. Teleportation is the transfer of just properties (a form of information) of one particle to another, not transportation of matter itself. This is a clever application of entanglement so make sure you have read that section first.
An example of how teleportation works:
I produce two entangled photons and send one to New York (photon A), and the other to Japan (photon B). Before any measurements are made on either photon, I entangle photon A with another (photon C) at the lab in New York. In doing so photon A is completely destroyed. As no measurements have been made then photon B instantly becomes entangled with photon C. Therefore the properties (information) of photon C are transferred to Photon B in Japan without ever interacting with it. Einstein was right: quantum physics is spooky.
I recommend you have that Jaffa cake now and have a lie down.
Quantum communication has the potential to provide secure encryption both by genuine random number generation, and by encryption methods that identify attempts at unwarranted snooping.
Quantum physics prohibits cloning of quantum states, so transmission of these states over long distances is difficult as you cannot amplify the signal. Teleportation offers a solution through quantum repeaters in which several particles are entangled in a long chain, through which information can be teleported from one end to the other.

Image credit: iStock.com/ Daniel Chetroni
Qubits
In digital electronics, information is encoded, manipulated and transmitted in the form of a bit. This is generated essentially with a switch that has only two states – on or off – that produce a change in voltage within a circuit25. All modern computing is possible with millions of these simple switches turning on an off at the right time. Digital communications use optical or radio frequencies which are modulated between two states to transmit bits.
Both quantum communications and quantum information processing use the quantum version of a computer bit – the qubit – to transmit and manipulate data. A qubit also has two states, but can also exist in all possible states in between these, which is where their strength lies. The actual state depends on the physical qubit being used. Examples include:
- the wave nature of a photon qubit could be oscillating up-down (state 0) or side-to-side (state 1)
- an electron qubit could have it’s ‘spin’ point up (state 0) or down (state 1)
- an atom could be in a low energy level (state 0) or high energy level (state 1)
What makes qubits different from classical bits is that they can be in a superposition of both states at the same time, whereas classical bits cannot. Moreover, when we measure a classical bit, the measurement does not affect the state of the bit. With a qubit, the measurement acts to irrevocably alter the qubit state. So why is this useful?
- A qubit contains both information about its state and the superpositions between states, whereas a bit only contains information on its state. Therefore qubits can hold more information.
- It is possible to create superposition of many qubits – each depending on one another. This leads to massive parallelism. This means that a quantum computer can explore all possible outcomes simultaneously, whereas a classical computer would need to explore each outcome one-by-one.
- This is possibly the most important point. Nature is fundamentally quantum, so a quantum computer reflects how reality actually is (with all the uncertainties and randomness) whereas a classical computer can only provide an approximation to reality.
Quantum information processing can require ‘stationary qubits’ that perform the calculation or act as a memory, or ‘flying qubits’ that transfer information between processing nodes. In the tunnelling section we learnt that quantum computers can work via annealing, but more general (or universal) quantum computers use quantum circuits which are more like classical digital circuits, albeit with entanglement and superposition thrown in for good measure!
Quantum computing has seen a lot of investment recently and developments are reaching the ‘quantum supremacy’ point where calculation speeds are beginning to outperform classical computers (for very specific tasks).
Quantum computers will complement, not replace classical computers as they are optimal for only certain types of calculations, such as searching databases, or finding prime numbers. Efforts are underway to find more applications and algorithms that have academic and industrial applications.

Two switches, one in the on position labelled 1, and one in the off position labelled 0
04 Wrapping up
I hope this tea-time jaunt through the world of quantum physics has provided you some insight into what makes this area of technology interesting and exciting, but has also de-mystified the subject. I also hope your tea has not gone too cold whilst your imagination was on this journey through the weird quantum landscape. It is strange, unintuitive and downright confusing, even for a physicist like me, but that is what makes it interesting and stimulating. But one thing I hope to have made clear is that it is not magic.
In a few decades from now we expect that quantum physics will be just another tool in the engineer’s repertoire to solve technical challenges, much like optical engineering or microelectronics have become embedded and familiar in our society. At Dstl, we see quantum technology as a key enabler for ‘generation after next’ technology. This is necessary to anticipate both opportunities and threats quantum technology may pose to the security and defence of the UK in future years.

Image credit: iStock.com/ XH4D
Interested in working with the Quantum Team at Dstl?
We are exploring all aspects of quantum technology across all areas including: sensing, timing, communications, imaging and information processing. We have a state of the art laboratory to understand first-hand how this exciting area can benefit UK defence and security. We are also interested in developing engineering solutions for operating quantum technology outside of the laboratory, on a number of platforms, and in different types of operations and environments.
Please get in touch at: quantum@dstl.gov.uk
Footnotes
-
Legally, it’s defined as a cake. ↩
-
When scientists use the term ‘theory’ we mean a reliable, mathematically rigorous and well-tested model of some effect. This is different from ‘hypothesis’ which is what we pose when coming up with a, as yet untested or complete, theory. ↩
-
From The Hitchhiker’s Guide to the Galaxy. ↩
-
The word ‘quantum’ comes from the latin quantus meaning ‘how great’. Its contemporary meaning is ‘a (small) discrete packet’. Therefore if you hear the oft used phrase “a quantum leap” it technically means ‘a tiny step’. ↩
-
A grain of salt contains around a million, million, million (1018) atoms. ↩
-
We can calculate the probabilities: you have approximately a 1 in 45,000,000 chance of being a winner and, unfortunately, a 44,999,999 in 45,000,000 chance of being a loser. ↩
-
The particle’s state must be reset before repeating the measurement otherwise one would keep measuring the same result over again. ↩
-
This refers to some property of the particle that can change in time and space. A degree of freedom might be position, direction of motion, energy, etc. It can also be the state of the atom. Essentially any property that is distinctly different and independent of other properties. ↩
-
Electrons orbitals have a range of shapes from spherical and dumbbell shaped, to very odd geometries resembling balloon sculptures. ↩
-
It is common to think of electrons whizzing around a nucleus like planets around the sun. This is not reality because electron’s positions are difficult to define to a single point when bound to an atom due to the uncertainty principle. A better way to think of orbitals is as fuzzy clouds indicating where the electron probably exists. ↩
-
This can be via eyesight or heat felt on the skin. ↩
-
Try waving your arms up and down, you need to exert more energy to flap faster (and look sillier). ↩
-
There are many types of transitions within an atom, some are more sensitive to the environment than others. The quantum engineer chooses a suitable transition for their intended application. ↩
-
Which we say is ‘entangled’ because we can’t know the state of one without knowing the state of the other. ↩
-
There’s a fun extension to this called ‘Wigner’s friend’. What if Schrödinger looked in the box but told no one what he saw; is he now entangled with the box, poison and cat? The big, confusing, question then becomes “what is a measurement in quantum mechanics?” ↩
-
Fuzzy, not furry. ↩
-
There are several experiments looking for this boundary, if it exists at all. Each year larger and larger particles are shown to have quantum properties. There may be no distinct barrier or, hopefully, some new and interesting physics that causes wavefunctions to collapse. ↩
-
Note that there only needs to be the opportunity for interaction to occur for decoherence to happen, as opposed to the interaction actually occurring. This is why quantum experiments are hard! ↩
-
A common interpretation is that we, as humans, have an effect on reality as ‘observers’. As discussed earlier in the decoherence section, the quantum process is only affected by information being extracted and so there is nothing special about who is doing it, nor how. ↩
-
You would still need to ‘average’ out the remaining noise to get the most accurate measurement, but using a squeezed state allows you to achieve the best possible measurement in the shortest time. ↩
-
This means that if I repeated the experiment I may get different probabilities of finding for heads or tails, but each of the results would only vary between 45% and 55%. ↩
-
It is a bit like receiving a book in an unknown foreign language, then having to wait for the translated book to read it. ↩

