Guidance

Quality assessment in data linkage

Updated 16 July 2021

James Doidge^1,2,3, Peter Christen⁴ and Katie Harron²

¹Intensive Care National Audit and Research Centre, London, UK

²University College London (UCL) Great Ormond Street Institute of Child Health, UCL, London, UK

³University of South Australia, Adelaide, Australia

⁴Research School of Computer Science, The Australian National University, Canberra, Australia

Contact: James Doidge

1. Introduction

Data linkage is fundamentally a balancing act; one of maximising the accuracy of linkage and validity of analysis within the constraints of human and computing resources and the quality of the available matching data. As with missing data, it is impossible to avoid making assumptions about linkage error. Our responsibility, therefore, is to make the best use of available information to inform those assumptions and assess their plausibility and potential influence on any conclusions we wish to draw. The inherent limitations of the tools available to assess the quality of linked data, the complex effects of linkage error on analysis, and the divide that too often exists between data linkers and data analysts, have each impeded the development of relevant methodologies and contributed to a general under-appreciation of the potential impacts of linkage error. This chapter outlines some fundamental concepts relating to linkage error and summarises the techniques available to both data linkers and data analysts for addressing it. We draw on examples primarily from the health literature, though the principles apply to a range of contexts. Achieving best practice in linkage quality assessment will require greater levels of engagement and information sharing between data collectors, data linkers and data analysts than is generally seen at present. Important requirements for information generation and sharing during linkage are summarised in a list of recommendations for data linkers and data analysts alike.

2. Linkage and linkage error

There are three broad categories of linkage methods: deterministic (rule-based) methods, probabilistic (score-based) methods, and techniques that make use of advanced machine learning algorithms. These approaches are usually treated as distinct methods, but in reality the methods overlap and have similar implications for linkage error and analysis.[1] The aim of each is to classify record pairs according to their true match status (whether they belong to the same person or entity), and they achieve this principally using information derived from matching variables that records have in common, such as names and dates of birth. In what follows, we use the term ‘match’ to refer to the true relationship between a pair of records, ‘link’ to refer to their derived or assumed classification, and ‘agreement’ to describe their similarity in terms of matching variables.

2.1 Deterministic linkage methods

Deterministic or rule-based methods are the most straightforward approach to linkage and typically make use of a pre-determined set of rules for classifying pairs of records as belonging to the same individual or not. For example in national hospital data in England (Hospital Episode Statistics), admissions for the same individual over time are linked using a three-step algorithm involving combinations of date of birth, postcode, sex, NHS number and the local patient identifiers used by hospitals.[2] More complex deterministic methods may incorporate the use of partial identifiers (e.g. postcode prefix or first letter of surname), phonetic codes (such as Soundex), or transposition of elements such as for date of birth.[3] These methods, along with similarity scores, or distance based measures (for example Mahalanobis distances) can also be incorporated into deterministic linkage rules (as well as probabilistic and machine learning methods).

2.2 Probabilistic linkage methods

Probabilistic linkage methods work by assigning a match weight (essentially a score) to represent the likelihood that two records belong to the same individual. In effect, this results in a ranking of all possible agreement/disagreement patterns (or equivalently, deterministic rules) for a set of available identifiers.[1] If training data (a representative set of record pairs with known match status) are available, then match weights can be estimated using any statistical or algorithmic technique for predicting binary classification. However, while clerical review (human decisions about the match status of different pairs of records) is sometimes used to generate training data for these purposes[4, 5], it is limited by the quality of the matching data available to support it and the lack of training data available from other sources. In the absence of training data, most approaches for deriving probabilistic match weights are based on the framework first formalised by Fellegi and Sunter, which can be seen as a Naïve Bayes approach due to assumptions about independence between identifiers.[6]

At the heart of the Fellegi and Sunter approach lie so-called likelihood ratios; ‘so-called’ because, in the absence of training data, they are estimated rather than calculated and may deviate from the likelihood ratios that would be observed if match status was known. These estimated likelihood ratios are constructed using estimated conditional probabilities of observing agreement on each matching variable; the ‘m-probability’ of agreement on an identifier, given two records belong to the same individual and the ‘u-probability’ of agreement, given the records belong to different individuals.[6, 7] Estimation of these conditional probabilities in the absence of training data (usually by an EM algorithm), and specification of overall likelihood as a function of agreement on individual matching variables, both require assumptions that may not be met in practice. Precisely which assumptions are required, and how resistant results are to their violation, depend on how the likelihood ratios are ultimately used. Use of likelihood ratios to estimate match probabilities for use in linkage quality assessment requires stronger assumptions than the more common use of logged likelihood ratios (match weights) for ranking of candidate links.[8] In the latter, linkage results appear relatively resistant to misspecification of likelihood functions.[9] An alternative unsupervised method, employing a scaling algorithm originating from correspondence analysis, has been developed to overcome some of the limitations of conventional techniques.[10] The scaling algorithm assigns scores to discrete categories of agreement/disagreement based upon minimisation of a suitable loss function but has undergone limited validation and development to date.

2.3 Machine learning based linkage methods

With recent advances in machine learning methods, alternative methods for both supervised and unsupervised classification methods (with or without training data, respectively), have found their way into the domain of data linkage.[11] While supervised techniques typically classify each record pair individually, so called `collective’ linkage techniques consider whole clusters of linked records (such as several individuals living at the same address) with the aim to find an overall optimal and consistent linkage solution for an entire database.[12] Unsupervised machine learning techniques, on the other hand, are mostly employed in linkage situations where multiple records of the same individual might exist (for example all hospital records for the same patient), or where records from groups of individuals need to be linked (such as all babies born to the same parents) [26, 40].[13, 14] Based on the similarities calculated between the compared records, and taking both these similarities as well as other links into account, the objective of such clustering methods is to identify all records that correspond to the same individual (or group of individuals) and insert them into one cluster, such that at the end of this process each individual (group of individuals) in a database is represented by a single cluster.

If sufficient training data are available, then machine learning based methods may be able to achieve higher quality than deterministic or conventional probabilistic linkage methods, but large-scale comparisons under varying conditions are largely missing from the literature.[11, 15] Ultimately, the quality of the available matching data and the availability of human and computing resources are bigger determinants of linkage quality than the choice of framework for approaching the problem. Within each framework (deterministic, probabilistic, and machine learning), there exists a wide spectrum of complexity. More complex algorithms can provide a finer degree of discrimination between record pairs or clusters, but choices made at any point in design or implementation can affect the quality of linkage outputs.

2.4 Linkage error and linkage quality metrics

False links occur when different individuals share the same identifiers or where identifiers are not sufficiently discriminative. Missed links can occur due to recording errors, genuine changes over time, or where missing or insufficiently distinguishing identifiers prevent a link from being made. The level of linkage error depends on the quality and completeness of the identifying data available within a data set, and can occur irrespective of the linkage methods employed.[1] In all linkage methods, some choice must generally be made about an evidentiary threshold for classifying record pairs as links or not. Decisions about classifying record pairs usually take into account the likelihood of both false links (where records belonging to different individuals are linked together) and missed links (where records belonging to the same individual are not linked), but the balance between the two error types will depend on the requirements of the data.

Analogous to screening tests, linkage accuracy is typically a trade-off between, on the one hand, sensitivity or recall (the proportion of true matches that are correctly identified) and on the other hand, specificity (the proportion of true non-matches that are correctly identified) or precision (the positive predictive value or proportion of assigned links that are true matches); see Table 1. All of the parameters that can be derived from these 2×2 tables (sensitivity/recall, positive predictive value/precision, etc) can be expressed as overall values (considering all possible links) or as marginal values conditioned on things such as agreement on blocking variables, match weight, or pattern of agreement. Both overall and marginal values are useful. Overall precision, for example, provides an estimate of the proportion of all links that are true, which can be used to correct for linkage error.[16] Marginal precision, if conditioned on pattern of agreement or match weight, provides an indication of the probability that those specific links are correct.

	True match (pair from same individual)	True non-match (pair from different individuals)
Predicted link	True link (true positive) a	False link (false positive) b
Predicted non-link	Missed link (false negative) c	True non-link (true negative) d

Table 1: Measures of linkage accuracy

In Table 1, sensitivity (or recall) = a/(a+c); specificity = d/(b+d); positive predictive value (or precision) = a/(a+b); negative predictive value = d/(c+d). Records in a and d are sometimes referred to as true matches and true non-matches; records in b and c are sometimes referred to as false matches and missed matches. The number of true matches is typically much smaller than the number of comparison pairs (for instance, the size of the Cartesian join of two data sets or the number of record pairs compared following blocking) and so the number of record pairs in d will usually be relatively large. Therefore, negative predictive value and specificity are typically high, and less informative than sensitivity or positive predictive value. The number in d can be derived from the total number of comparisons and the numbers in a, b and c.

In some situations, maximising sensitivity (recall) will be a priority. For example, if the purpose of linkage is to provide follow up for a set of individuals who may have been exposed to an infectious disease, it will be important to identify all possible matches, possibly at the expense of including some false links (which could be excluded later on further detailed inspection of records). More often, specificity (or positive predictive value/precision) will be prioritised, at the expense of missing some true matches. For example, if linkage is used to identify a sample of individuals to be contacted about a sensitive health condition, then it will be important that no false links are made. While more complex linkage algorithms can provide better discrimination between true matches and true non-matches, there is generally an inescapable trade-off between precision and recall (or any other ways of measuring false links and missed links) among any uncertain links that cannot be classified as definite matches or definite non-matches.

There are also circumstances in which the aim is to minimise the total number of errors, for example when estimating the rate of a condition in the population. In this scenario, an optimal single threshold may be chosen to either minimise the sum of errors (false links + missed links) or minimise the net effect of errors (false links – missed links). The F-measure (the harmonic mean of precision and recall: f = (2 * precision * recall) / (precision + recall)) is a metric commonly employed in machine learning to evaluate imbalanced classification problems, which has also been used in the context of data linkage for deriving a single number measure of linkage quality. However, as recently shown by Hand and Christen,[17] the F-measure has methodological problems when it is used to compare different data linkage classifiers; namely that it depends on the match rate of the different classifiers used. The F-measure is therefore not recommended in the context of evaluating data linkage quality. Hand and Christen [15] propose some more appropriate alternatives.

Decisions on the most appropriate classification of record pairs are ideally made on a study-by-study basis, depending on the likely effects of linkage errors and any arising bias for a particular analytical output. If linkage is conducted without knowledge of the intended analysis or to support multiple analyses, then the linkage outputs must support a range of preferences about linkage error. This can only be achieved by retaining less-than-certain links and generating link-level measures of agreement or accuracy (e.g. match weights or estimates of marginal precision) for use by analysts. With these outputs, end-users are able to effectively tune linkage algorithms and implement sensitivity analyses without requiring access to identifiers.

2.5 The many manifestations of linkage error

The ultimate goal of linkage quality assessment is to understand the implications of any linkage error for the intended application - usually some sort of analysis of linked data. While there may only be two types of linkage error, the implications of these for analysis can be devilishly complex. Depending on how the linked data are analysed or interpreted, linkage error may lead to missing data (in variables obtained through linkage), misclassification or measurement error (incorrect values of variables for analysis) or to erroneous inclusion or exclusion from a data set (for example, if a linkage variable has been used to define the analytic sample). It can also lead to strange combinations of these phenomena where one person’s records are ‘split’ and counted as if representing multiple people, or multiple people’s records are ‘merged’ and counted as one. In each of these instances there is usually some degree of accompanying measurement error or missing data in the person-level variables, particularly measures of the number of records per person or the time between events. Further explanation of these concepts can be found in Doidge and Harron.[18] To understand how linkage error could influence a given analysis, it helps to consider the following questions:

1. Are links being meaningfully interpreted (is the presence or absence of a link used to imply the value of some variable for analysis)? A common example of meaningful interpretation is the classification of vital status from linkage to a register of deaths.
2. Is linkage being used to determine inclusion in an analytic sample, as in could linkage error result in people being erroneously included or excluded from analysis? If so, then it is worth considering the implication of linkage error for selection bias.
3. Could linkage error lead to splitting of one person’s records into many or merging of multiple people’s records into one?

Merging and splitting can have implications in many situations, especially but also regardless of whether totals are to be estimated. Whenever splitting or merging are implicated, we need to consider not just the accuracy of classification in individual record pairs but the degree to which whole clusters of linked records (e.g. all the records assumed to relate to one person) accurately represent the ground truth set of people or other entities. The techniques below focus on assessing linkage quality at the level of record pairs and these are followed by further discussion of how to assess linkage quality in terms of clustering.

Despite the many possible manifestations of linkage error, there is one universal factor that can determine the strength and direction of linkage error bias: the distribution of linkage errors with respect to variables of interest (variables relevant to a given analysis). If missed links or false links are more common in one subgroup than another, then any analysis of that subgroup or variable is at risk of significant bias. There are many common analysis variables (or ‘payload’ variables used for analysis but not always for linkage) that are known to be commonly associated with linkage error, including age, gender, ethnicity and socioeconomic status.[19, 20] For these associations to be accounted for in analysis of linked data, analysts need to be equipped with linkage outputs that enable them to explore the distribution of linkage errors with respect to any variables that they might be interested in - including variables that data linkers might not have access to (because of separation between identifiers required for linkage and the payload data required for analysis) or that don’t even exist until the analyst constructs them in the linked data. The following section describes various techniques for linkage quality assessment that may be available to data linkers, analysts or both, highlighting the information that is required for each.

3. Linkage quality assessment

Uncertainty in data linkage, particularly with administrative data, is generally inescapable. If the accuracy of links could be assessed with certainty, then that process for assessing accuracy would likely be incorporated into the linkage algorithm itself. Every conceivable technique for linkage quality assessment is either a partial measure (it only identifies some errors) or indirect (it only estimates the rate or distribution of errors). Data providers, ethics committees and information governance authorities may be uncomfortable with the idea of uncertainty about the identity of records, but it is something we have no choice but to accept and accommodate. The present push toward minimising collection and processing of personal data is increasing uncertainty in data linkage (through fewer available matching variables) and, counterproductively, hampers implementation of consent-based approaches to data use (if there is uncertainty about which records belong to which people, then how can you know if you are processing their data or excluding records for people who opt out of data sharing?).

While we are unable to measure linkage accuracy directly or completely, there are a range of techniques that can be implemented to gain some information about linkage quality. Some require access to identifiers, but many can be implemented by data analysts so long as they are provided with the right, pseudonymised, outputs from linkage. It is important that some of the assessment be conducted by analysts so that the likely distribution of linkage errors with respect to their analysis variables can be established.

There are three vital pieces of information that need to be derived from quality assessment: estimates of the rates of missed links (1 - recall) and false links (1 - precision; see Table 1), estimates of how these errors influence clustering, and estimates of how errors vary according to any variables of interest for a given analysis. Some techniques identify likely or definite linkage errors. While it is possible to correct or exclude these, these records also contain potentially valuable information about the distribution of errors with respect to analysis variables, which may be generalisable to the errors that were not detected. It is therefore important that this information is not discarded but retained for interrogation by the data linker or analyst. Table 2 summarises the information required to implement each technique for linkage quality assessment and the information about linkage quality that it can produce. Specific techniques are explained further below.

Identifier needed?	Technique	Required inputs	Potential outputs
Yes	Training data (gold standard)	Identifiers	Rates of missed links and false links and/or distribution of error rates
Yes	Clerical review	Identifiers +/- supplementary matching data	Human estimation of match status leading to estimated rates of false links and distribution of false links
Yes	Negative controls	A set of records not expected to link that can be submitted to the linkage procedure	Rates of false links
No	Unlikely or implausible links	Links excluded by data linkers during quality assurance; and/or records with multiple candidate links even when only one is possible; and/or payload data	Distribution of false links, rate of false links*
No	Analysis of matching variable quality	Record-level or aggregate indicators of matching variable quality	Identification of unlinkable records Distribution of missed links and/or likely missed links
No	Comparison of linked vs unlinked records	Unlinked records, or aggregate characteristics of unlinked records, when all records in one or both files are expected to have matches	Distribution of missed links Rate of missed links when expected match rate = 100%, given rate of false links can also be estimated
No	Positive controls	Unlinked records for a subset of records expected to have matches	Distribution of missed links Rate of missed links, when rate of false links can be estimated
No	Comparison of linked data to external reference statistics	Statistics derived from another representative data set for observable characteristics of the linked data	Rate of missed links* Rate of false links* Distribution of missed links* Distribution of false links*

Table 2: Techniques for linkage quality assessment

*The term ‘rate’ is used very loosely in this table to refer to any measurement of errors, and some outputs depend on the context (see further explanations of each technique below).

3.1 Training data (gold standard)

In some situations, ‘gold standard’ or training data are available, where the true match status of records is known. Such data are only ever available for a subset of records (or else linkage would not be required). Training data are sometimes derived from a subset of records that have additional information available for matching and can be used to estimate rates and distributions of linkage errors in the remaining records. For example, one study of infection rates among children in intensive care involved linking data from laboratories in England with information on paediatric intensive care admissions from a national audit data set.[21] Overall, only 51% of laboratory records included a unique person identifier (NHS number). However, two of the 22 laboratories were able to provide complete values for all identifiers. Gold standard linked data from these two laboratories were used to calculate the percentage bias in the outcome (infection rate) for a range of linkage strategies.

With sufficient training data, a whole suite of statistical models and algorithms can be thrown at the problem of record linkage, including advanced machine learning methods as discussed earlier. The main obstacle to these is identifying a representative set of records in which link status is known. When gold standard data are used to train linkage algorithms, the set are assumed to be representative in terms of the joint distribution of errors and natural discrepancies in the values of matching variables. When gold standard data are used to assess linkage quality for analysis of linked data, the set are assumed to be representative in terms of the joint distribution of matching variable quality and any analysis variables. In practice, training data often struggle to meet these ideals and the extent to which they do is generally untestable. For example, if based on a previous linkage (even deterministic based on some unique person identifiers such as NHS number), there may be errors in these identifiers or the set with identifiers may not represent the remainder. If based on manually classified record pairs (for example clerical review), then even experienced domain experts may make mistakes and stand little chance of identifying true matches in the presence of substantial missing data.[22]

3.2 Clerical review

One approach that is commonly used to generate a gold standard is clerical review (human decision-making about link status). Other than being resource-intensive, the main limitation of clerical review is the data available to support it. Humans can only outperform linkage algorithms if provided with sufficient or supplementary matching data (e.g. original handwritten records, or additional variables). If the matching data are insufficient (e.g. missing) then neither human nor algorithm will be able to accurately classify match status. The sheer number of non-matching record pairs is another factor; nearly always limiting clerical review to pairs linked by an algorithm or those classified as likely candidates (e.g. having match weights just below the threshold for acceptance). Matching pairs that have substantial missing data or substantially inconsistent data will be thoroughly hidden in the proverbial haystack of non-matches and never submitted for review. For these reasons, clerical review is more useful for estimating precision (by identifying false links) than for estimating recall (identifying missed links).[23]

Recent research in the area of active learning has investigated how manual domain expertise can be combined with supervised machine learning algorithms.[24] Rather than conducing a clerical review after an initial algorithmic classification, samples of difficult to classify record pairs are given to a domain expert for manual assessment, and the resulting set of classified examples is combined into a training data set that is used to train a supervised classifier. Over several iterations, as the training data gets larger and its representativeness gets better, increasingly more accurate classification models can be built. Experiments have shown that even with a few hundred manually assessed examples linkage quality comparable to fully supervised machine learning classifiers can be achieved.[24] In effect, carefully targeted clerical review can be used to reduce the amount of training data (or clerical review) required. As above, these techniques remain limited in the capacity for estimating recall.

3.3 Negative controls

Negative controls are records that are known not to have matches but are intentionally submitted to the linkage process to assess the rate of false links. For example, a study linking maternal mortality records with birth records used a subset of women who were known to have had an abortive outcome (and therefore should not link with a live birth within a physiologically implausible time period) as negative controls.[25] Of the 1046 records with abortive outcomes, 124 linked with a birth record, providing an estimated specificity of 88%. Similarly, Moore et al. [26] assessed the specificity of linkage to a register of deaths among a subset of prisoners known to be alive at the end of the study period. Time and date dimensions often create implausible combinations of records. This approach to estimating specificity relies on being able to identify a set of non-matching records that is representative in terms of matching variable quality, and requires a high degree of confidence in the quality of timestamps or other variables that imply implausibility. Provided that the information governance framework supports the use of negative controls (for instance, records that may be only indirectly relevant to an intended analysis), negative control records can be submitted alongside the rest of records to be linked.

3.4 Unlikely or implausible links

While negative controls require identification of whole sets of records known to be non-matches, there are often other opportunities for identifying more specific implausible combinations of values, or from implausible combinations of links themselves. For example, it may not be plausible for simultaneous events to be linked, for events to occur before birth or after death, or there may be a maximum plausible number of records that can be associated with any one individual. Whereas negative controls are identified in advance of linkage, these implausible scenarios are identified after the initial linkage process. When identified by data linkers, they may be excluded from the linked data in the name of ‘quality assurance’. However, these records can provide potentially valuable information, as the identified links are generally the tip of a hidden iceberg of false-but-plausible links. If retained and interrogated, the identified implausible links can be used to inform assumptions about the distribution of unidentified false links and may even support estimation of the total number of false links or the marginal level of precision.

For example, a study linking longitudinal hospital records found that some individuals appeared to have been born twice or had been admitted following death. By investigating the characteristics of individuals who appeared to have been simultaneously admitted to hospitals in different parts of the country, the authors found that false links were associated with health status (preterm birth) and ethnic group.[27] Even though only a fraction of all false links would have had been implausible, the information derived from those would be valuable for interpreting any analysis of preterm births or ethnicity in the linked data, even after excluding those identified false links.

When multiple records are linked, they form a cluster of records.[14] Clusters are defined by records (nodes) and the relationships (links, or edges) that exist between them. There are many examples of implausible clusters, perhaps the most common of which occur in one-to-one or one-to-many linkages where at most one record from one or each file is expected to be included in each cluster. Under these restrictions, the presence of multiple candidate links that have equivalent or sufficient level of agreement to each be accepted implies that at most one of those candidate links is true. One-to-one and one-to-many linkage algorithms are usually designed to exclude all candidates in the presence of such ambiguity, but analysing the number and characteristics of ambiguous links can reveal information about the number and distribution of false links. For example, Blakely and Salmond [28] show how these ambiguous links can be used to estimate the marginal level of precision at different levels of probabilistic match weight.

More complex examples of cluster plausibility can be derived using graph metrics, which show the ‘shape’ of link clusters. For example, two cohesive clusters of links, in which each record links to each other record and the two clusters are joined by a single link (a ‘bridge’) may indicate a false link. See Randall et al. [29] for further examples and metrics.

Finally, it is worth highlighting that some false links can only be identified by implausible combinations of ‘payload’ variables that data linkers may not have access to. These present an opportunity for data analysts to feedback information about linkage quality to data linkers and thereby support enhancement of the data set and/or linkage algorithm. Data linkage units would be wise to encourage and systematise processes for receiving this information and incorporate it into subsequent refinements of the data set and algorithm.

3.5 Analysis of matching data quality

Analysis of the quality of matching data in individual records may be the lowest hanging fruit in terms of linkage quality assessment; it is straightforward and possible to implement in every linkage scenario. By examining the pattern of missing or invalid matching values, it is often possible to identify records with insufficient data for linkage; these will definitely not be linked and so, if expected to be linked, will place a known limit on the achievable level of recall. They can also be interrogated to infer the likely distribution of missed links within their data set. Records with low quality but technically sufficient matching data may be more likely to be implicated in both missed and false links, so analyses of these could provide evidence about the distribution of both. For example, when analysing records from the Hospital Episode Statistics (HES) for England database, we know from examining the current HES patient ID (HESID) algorithm (the linkage algorithm that assigns unique patient identifiers) that any records that are missing NHS number plus any one of date of birth, postcode or sex, will have been impossible to link to any other records in the database.[30] We also know that records with missing NHS numbers (but complete data in the other matching variables) are more likely to be implicated in both missed links (because postcodes may change over time) and false links (because twins may share dates of birth, postcodes and sex). By examining the characteristics of such records, researchers have been able to identify differences in linkage error over time, and by age, gender, social status and health status.[31, 32] For analysts to be able to assess the likely distributions of linkage error with respect to their variables of interest, we recommend that record-level or aggregate indicators of missing or invalid matching values be routinely included with every linked data set.

3.6 Comparison of linked vs unlinked records

Comparing the characteristics of linked and unlinked records can provide evidence about the distribution of missed links with respect to any set of variables. For example, a study of linkage between mother and baby hospital records compared a range of characteristics (including birth weight, maternal age, and perinatal outcomes) between linked records (n = 250,186) and unlinked maternal records (n = 3,798) and unlinked infant records (n = 2,596).[33] Despite 99% of records being linked, there were important differences in characteristics that could introduce bias into analyses: stillbirths and preterm births were over-represented in the unmatched records, as were Australian-born mothers and births in private hospitals. This kind of comparison therefore provides information on the groups of records that might be most affected by linkage error (for example due to differing data quality) and therefore on the distribution of linkage errors with respect to important analysis variables.

Where it is not possible for data linkers to release record-level information on unlinked records, producing aggregate characteristics of unlinked records (as presented in the Australian analysis) is also helpful in identifying potential sources of bias (in the same way as the above section on matching data quality). This would require that data linkers have at least some payload information on the variables of interest (for instance survival status, or age and gender).

Comparing the characteristics of linked and unlinked records is only relevant when all records in the primary file are expected to have a link (for example, a perfectly overlapping linkage structure).[18] This is a relatively uncommon scenario, and it is often the case that we do not know a priori how many records will link (for instance when linking a cohort to a mortality file). Even when we are linking whole populations, migration or incomplete follow up may mean that the number of expected links is unknown. However, even in these scenarios it may still be possible to identify a subset of records that are expected to match (‘positive controls’) or are known to definitely not have a match (‘negative controls’).

3.7 Positive controls

In one study linking a cohort of prisoners to a register of deaths, the researchers used a subset of prisoners who were known to have died in prison as positive controls.[26] They found that of the 311 prisoners known to have died, 36 were not linked so would otherwise have been recorded as alive using their linkage algorithm; an estimated sensitivity of 88%. Deriving estimates of sensitivity from a match rate in this way requires an assumption about the level of false links that may also be contributing to the match rate. Depending on the quality of matching data and design of the linkage algorithm, it may be reasonable to assume that the number of false links is negligible for these purposes. Otherwise, it may be more reasonable to incorporate specific assumptions about non-zero levels of false links and deduct these from the observed match rate to estimate sensitivity. Ultimately, it is the level of overall misclassification in analysis variables (such as mortality) that matters, rather than the numbers of missed links and false links that contribute to this.

3.8 Comparison of linked data to external reference statistics

Comparing the characteristics of the linked sample of records with external reference statistics can provide evidence about the rates or distributions of missed links or false links. For example, a study linking the Swiss National Cohort study with mortality records compared the age-sex-specific mortality rates derived from the linked data with those from official midyear population data, and found that underestimation of mortality rates (due to missed links) was more pronounced in older age groups.[34] Such analyses require that the external reference statistics were derived from a representative data set, and very careful consideration of any other possible explanations for any observed differences (especially differences in data collection or quality).

3.9 Assessing linkage quality in terms of clustering

While linkage quality assessment has historically focused on precision and recall, these link-based measures of accuracy ignore the fact that analysis of linked data typically occurs at the level of clusters of linked records rather than record pairs. One person (or other unit of analysis) is typically represented by a cluster of n linked records, containing n(n - 1)/2 links (including both the direct links created through record comparisons and any indirect links created by these when applying the transitive closure: if record pair (r1, r2) is classified a match and record pair (r1, r3) is also classified a match then record pair (r2, r3) must also be a match).[11] Precision and recall, while adequate for representing the accuracy of links, are insufficient for representing the accuracy of linkage in terms of clustering (Figure 1).[13]

Doidge and Harron [18] consider these concepts in terms of splitting (where records belonging to a single individual are ‘split’ and appear as multiple individuals) and merging (where records belonging to different individuals are ‘merged’ and appear to belong to a single individual), and discuss the importance of understanding the rates at which missed links and false links lead to each of these. Nanayakkara et al. [13] propose a set of supplementary parameters for operationalising linkage quality with respect to clustering and show how the optimisation of linkage algorithms should account for these. The authors propose an evaluation method that is complementary to estimating precision and recall, based on evaluating the classification of records as linked clusters rather than individual links. This approach aims to identify clusters of linked records that best represent ‘ground-truth’ clusters and defining correct classification of records according to membership of that cluster.

Techniques for estimating and using these parameters in linkage quality assessment remain a topic for further development and one that data linkers and analysts should consider in light of the intended application.

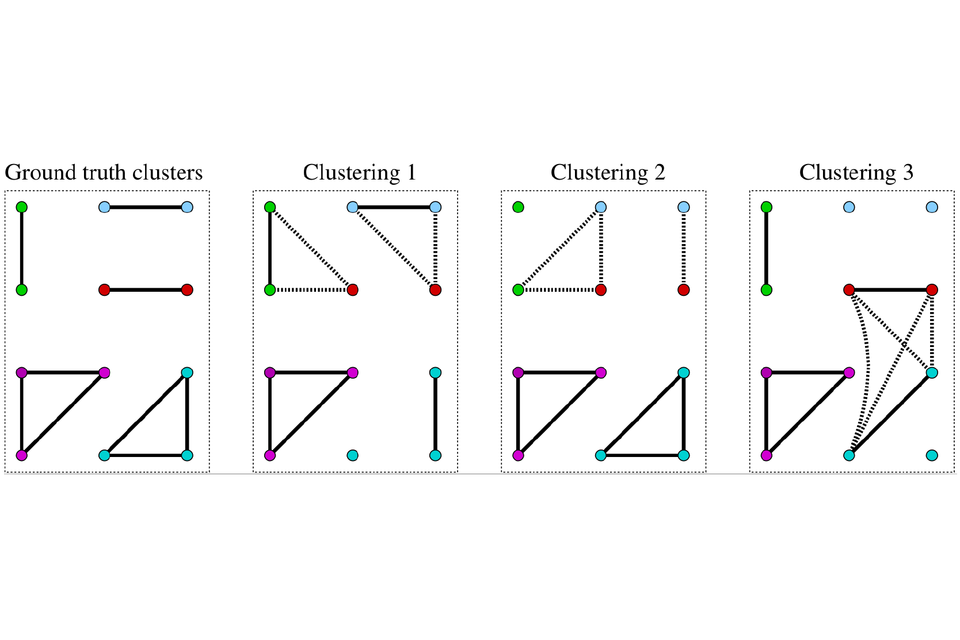
Figure 1: Impacts of linkage error on clustering.

In Figure 1, node colours represent the five true record clusters, solid edges true matches, and dotted edges show false links. The three linkage results (clusterings) have identical match rates, precision and recall but different implications for analysis of the linked data. Figure reproduced from Nanayakkara et al. [13] under Creative Commons license CC-BY 4.0

4. Addressing linkage error in analysis of linked data

The relative novelty of large linked databases, the complex manifestations of linkage error, and the separation that too often exists between data linkers and data analysts have each contributed to impeding the development of statistical techniques for addressing linkage error. In 2020, we are arguably at a level of sophistication comparable to the point that techniques for handling missing data were at three decades ago; seminal papers are emerging, and awareness of the issue is rising but there is no purpose-built software and few analysts feel confident in addressing the issue. Here, we provide a brief overview of emerging methods and highlight the information requirements that data linkers should strongly consider generating and providing wherever possible. Techniques for addressing linkage error can be broadly grouped into:

• Sensitivity analysis in which the analyst varies the threshold for accepting record pairs as links, moving up or down the spectrum of agreement. To do this they require information about the match rank or match weight, or the patterns of agreement that underlie these. They also need uncertain links to be included in the data they are provided with. An example of sensitivity analysis for linkage error can be seen in Lariscy.[35] While sensitivity analysis is probably the most common example of analysis accounting for linkage error to date, it is also limited. There is generally a trade-off between missed links and false links (or recall and precision, or sensitivity and specificity [22]) and no point of zero linkage error anywhere on the spectrum of agreement. The range of analysis outputs produced from a range of link-acceptance thresholds is not guaranteed to encompass the true value of any target parameter.
• Probabilistic analysis in which match probabilities are input into multiple imputation [21, 36] or inverse probability weighting [37, 38] models. Probabilistic analysis requires access to uncertain links and estimates of match probabilities that may be hard to estimate. A second limitation of these techniques (one that is likely to be addressed in future development) is the complications that arise when the unit of analysis is affected by clustering (e.g. when two records are counted as one person if linked and two people if not). Early applications of these techniques have employed a range of approaches to estimating match probabilities but have all been limited to one-to-one linkages in which the set of observational units is known prior to linkage. However, the potential value of the techniques and opportunities for further development are clear.
• Bias analysis in which estimates of the likely or plausible extents of linkage error are used to either make qualitative inferences about the strength and direction of linkage error bias, or to quantitatively adjust analysis outputs for its influence.[18, 39, 40] The capacity for bias analysis hinges on understanding the potential manifestations of linkage error for a given analysis: simple model-based estimates of linkage error are often insufficient.[41] However, the strengths of bias analysis lie in its flexibility; if empirical estimates of linkage error rates are unavailable then assumptions about these can be specified (see Doidge et al. [31] for an example of this). The main limitation is that for more complex analyses (regression models and so on), the formulae for adjusting for linkage error become similarly complex. In these cases, it may be advisable to simulate the assumed patterns of linkage error in the data themselves, prior to fitting analysis models. In this way, the distinction between bias analysis and probabilistic analysis becomes blurred. A fully probabilistic bias analysis would also account for uncertainty in the bias parameters (parameters defining the rates and distributions of linkage error) themselves.[42, 43]

5. Conclusions

Arguably the most difficult and important changes that are required of the data linkage community to improve the handling of linkage error are behavioural and perceptual. The structural separation between data linkers and data analysts is unlikely to disappear as it provides substantial benefits to privacy and confidentiality. But there are steps that we can take to help bridge the gap and create a more cohesive system that enhances the extraction of value from linked data.

In summary, data linkers are encouraged to:

• prior to linkage, engage with end-users of the linked data to understand their requirements in terms of the quality of data linkage and potential implications of both missed links and false links for the intended application
• be transparent about the approach taken to linkage, including data cleaning and harmonisation, assessment of agreement between records, use of clustering algorithms and quality assurance
• accept that linkage error is generally inevitable and that no single approach to linkage quality assessment is likely to be sufficient for measuring it
• find a balance between the quality needs of the intended application, the quality of the data available for linkage, and the resources available to support linkage.

Data analysts are similarly encouraged to:

• engage with data linkers to understand their approach to linkage and discuss expectations and desires in terms of linkage quality and outputs
• accept that linkage error is generally inevitable and likely to effect analysis in some way, but that it also cannot be measured directly so assumptions about it will be required
• find a balance between conducting linkage quality assessment, adjusting for linkage error in analysis, and all other aspects of administrative data quality that should be considered
• feedback identified linkage errors and other outputs of linkage quality assessment to data linkers to support development of the data set and linkage algorithm
• report on the quality of linkage to end users

To employ the methods for quality assessment described in the previous section, and ultimately to account for linkage error within analyses, analysts need specific information about how the linkage was conducted. Some of the methods can only be implemented by those with access to the identifiable data (for instance clerical review and linkage of gold-standard data). Other methods can be implemented within the de-identified, linked data that are provided to analysts following linkage, and sometimes are only available to analysts. Analysing the distributions of linkage errors that are relevant to any given application requires knowledge of and access to the analysis variables, some of which may not even be constructed until after linkage has taken place. How much of this quality assessment can be implemented therefore depends critically on what information is available to analysts.

At a minimum, linkage outputs should include:

• detailed information about the linkage process
• record-level information about matching variable quality (e.g. an indicator of whether each matching variable was missing, invalid or valid)
• link-level information about match quality (e.g. pattern of agreement, match rank, match rule, match weight or probability if estimated; such information is generally not disclosive or can be provided in a non-disclosive format)
• aggregate information about any identified linkage errors (for example, links excluded during quality assurance)

and, wherever possible, linkage outputs should also include:

• uncertain links
• record-level information about any identified linkage errors

Provided with sufficient information about linkage, there are a number of ways that data analysts can handle linkage error within analyses and generate stronger conclusions. Information on the (un)certainty with which records have linked can be used within a multiple imputation or probability weighting framework to properly represent uncertainty in results.[37, 44, 45] This information can also be used within sensitivity analyses that explore the types of records that are most affected by data quality and linkage error, to identify potential sources of bias.[44 - 46] Information on the rates and distribution of linkage errors according to important characteristics can be used to inform bias analysis, and produce results that hold under a specified range of assumptions.[31]

Guidance is available to help analysts determine what information they should present alongside analyses of linked data. The RECORD guidelines were created to provide guidance on the reporting of studies conducted using routinely collected data, and include a specific section on data linkage.[47] The GUILD guidance was created to raise awareness about the importance of communicating across the data linkage pathway, to improve the transparency, reproducibility and accuracy of linkage processes.[48] It is this communication that will ultimately ensure that we are able to overcome the obstacles posed by linkage error and unlock the full potential of linked data.

6. References

1. Doidge J and Harron K, Demystifying probabilistic linkage. Int J Popul Data Sci, 2018. 3(1).

2. Hagger-Johnson, G., et al., Data linkage errors in hospital administrative data when applying a pseudonymisation algorithm to paediatric intensive care records. BMJ Open, 2015. 5(8).

3. Christen, P., Data matching: concepts and techniques for record linkage, entity resolution, and duplicate detection. 2012: Springer: Data-centric systems and applications.

4. Goldberg, A. and A. Borthwick, The ChoiceMaker 2 Record Matching System. 2005, ChoiceMaker Technologies, Inc.

5. Christen, P. and K. Goiser, Quality and complexity measures for data linkage and deduplication, in Quality Measures in Data Mining. 2007, Springer. p. 127-151.

6. Fellegi IP and Sunter AB, A theory for record linkage. J Am Stat Assoc, 1969. 64(328): p. 1183-1210.

7. Sayers, A., et al., Probabilistic record linkage. Int J Epidemiol, 2015. 45(3): p. 954-964.

8. Chipperfield, J.O. and R.L. Chambers, Using the Bootstrap to Account for Linkage Errors when Analysing Probabilistically Linked Categorical Data. 2015. 31(3): p. 397.

9. Xu, H., et al., Incorporating conditional dependence in latent class models for probabilistic record linkage: Does it matter? Ann. Appl. Stat., 2019. 13(3): p. 1753-1790.

10. Goldstein, H., K. Harron, and M. Cortina-Borja, A scaling approach to record linkage. Stat Med, 2017. 36: p. 2514-21.

11. Christen, P., Data Matching: Concepts and techniques for record linkage, entity resolution, and duplicate detection. Data-Centric Systems and Applications. 2012: Springer-Verlag Berlin Heidelberg.

12. Bhattacharya, I. and L. Getoor, Collective entity resolution in relational data. ACM Trans. Knowl. Discov. Data, 2007. 1(1): p. 5–es.

13. Nanayakkara, C., et al., Evaluation measure for group-based record linkage. International Journal of Population Data Science, 2019. 4.

14. Draisbach, U., P. Christen, and F. Naumann, Transforming Pairwise Duplicates to Entity Clusters for High-quality Duplicate Detection. J. Data and Information Quality, 2019. 12(1): p. Article 3.

15. Elfeky, M., A. Elmagarmid, and V. Verykios, TAILOR: A Record Linkage Tool Box. 2002. 17-28.

16. Chambers, R., Regression analysis of probability-linked data, in Official Statistics Research Series, Volume 4. 2009: Wellington.

17. Hand, D. and P. Christen, A note on using the F-measure for evaluating record linkage algorithms. Statistics and Computing, 2018. 28(3): p. 539-547.

18. Doidge, J. and K. Harron, Reflections on modern methods: Linkage error bias. International Journal of Epidemiology, 2019. 48(6): p. 2050-2060.

19. Bohensky, M., Chapter 4: Bias in data linkage studies, in Methodological Developments in Data Linkage, K. Harron, C. Dibben, and H. Goldstein, Editors. 2015, Wiley: London.

20. Bohensky, M., et al., Data linkage: A powerful research tool with potential problems. BMC Health Serv Res, 2010. 10(1): p. 346-352.

21. Harron, K., et al., Linkage, evaluation and analysis of national electronic healthcare data: application to providing enhanced blood-stream infection surveillance in paediatric intensive care. PLoS One, 2013. 8(12): p. e85278.

22. Smalheiser, N.R. and V.I. Torvik, Author name disambiguation. Annual Review of Information Science and Technology, 2009. 43(1): p. 1-43.

23. Boyd, J.H., et al., A Simple Sampling Method for Estimating the Accuracy of Large Scale Record Linkage Projects. Methods of Information in Medicine, 2016. 55(3): p. 276-283.

24. Christen, V., P. Christen, and E. Rahm, Informativeness-based active learning for entity resolution, in Workshop on Data Integration and Applications. 2009, Springer: Würzburg.

25. Paixão, E.S., et al., Validating linkage of multiple population-based administrative databases in Brazil. PloS One, 2019. 14(3): p. e0214050-e0214050.

26. Moore, C.L., et al., A new method for assessing how sensitivity and specificity of linkage studies affects estimation. PLoS One, 2014. 9(7): p. e103690.

27. Hagger-Johnson, G., et al., Identifying false matches in anonymised hospital administrative data without patient identifiers Health Serv Res, 2014. 50(4): p. 1162-78.

28. Blakely, T. and C. Salmond, Probabilistic record linkage and a method to calculate the positive predictive value. International Journal of Epidemiology, 2002. 31(6): p. 1246-1252.

29. Randall, S.M., et al., Use of graph theory measures to identify errors in record linkage. Computer Methods and Programs in Biomedicine, 2014. 115(2): p. 55-63.

30. Health and Social Care Information Centre, Replacement of the HES Patient ID (HESID). 2009.

31. Doidge, J., et al., Prevalence of Down’s Syndrome in England, 1998–2013: Comparison of linked surveillance data and electronic health records. International Journal of Population Data Science, 2019. (in press).

32. Harron, K., et al., Linking Data for Mothers and Babies in De-Identified Electronic Health Data. PLOS ONE, 2016. 11(10): p. e0164667.

33. Ford JB, Roberts CL, and Taylor LK, Characteristics of unmatched maternal and baby records in linked birth records and hospital discharge data. Paediatr Perinat Epidemiol, 2006. 20(4): p. 329-337.

34. Schmidlin K, et al., Impact of unlinked deaths and coding changes on mortality trends in the Swiss National Cohort. BMC Med Inform Decis Mak, 2013. 13(1): p. 1-11.

35. Lariscy, J.T., Differential Record Linkage by Hispanic Ethnicity and Age in Linked Mortality Studies. Journal of Aging and Health, 2011. 23(8): p. 1263-1284.

36. Goldstein, H., K. Harron, and A. Wade, The analysis of record-linked data using multiple imputation with data value priors. Statistics in Medicine, 2012. 31(28): p. 3481-3493.

37. Chipperfield, J., A weighting approach to making inference with probabilistically linked data. Statistica Neerlandica, 2019. 73(3): p. 333-350.

38. Chipperfield, J., Bootstrap inference using estimating equations and data that are linked with complex probabilistic algorithms. Statistica Neerlandica, 2019. (epub ahead of print).

39. Lahiri, P. and M. Larsen, Regression analysis with linked data. JAMA, 2005. 100(469): p. 222-230.

40. Winglee, M., R. Valliant, and F. Scheuren, A case study in record linkage. Surv Methodol, 2005. 31(1): p. 3-11.

41. Newcombe, H.B., Age-related bias in probabilistic death searches due to neglect of the “prior likelihoods”. Comput Biomed Res, 1995. 28(2): p. 87-99.

42. Lash, T.L., M.P. Fox, and A.K. Fink, Applying Quantitative Bias Analysis to Epidemiologic Data. Statistics for Biology and Health, ed. M. Gail, et al. 2009, New York: Springer.

43. Lash, T.L., et al., Good practices for quantitative bias analysis. International Journal of Epidemiology, 2014: p. 1969-85.

44. Goldstein, H., K. Harron, and A. Wade, The analysis of record-linked data using multiple imputation with data value priors. Stat Med, 2012. 31(28): p. 3481-93.

45. Harron, K., et al., Evaluating bias due to data linkage error in electronic healthcare records. BMC Med Res Methodol, 2014. 14(1): p. 36.

46. Rentsch, C.T., et al., Impact of linkage quality on inferences drawn from analyses using data with high rates of linkage errors in rural Tanzania. BMC Medical Research Methodology, 2018. 18(1): p. 165.

47. Benchimol, E.I., et al., The REporting of studies Conducted using Observational Routinely-collected health Data (RECORD) Statement. PLoS Med, 2015. 12(10): p. e1001885.

48. Gilbert, R., et al., GUILD: Guidance for Information about Linking Data sets. J Public Health, 2017. 1-8.